
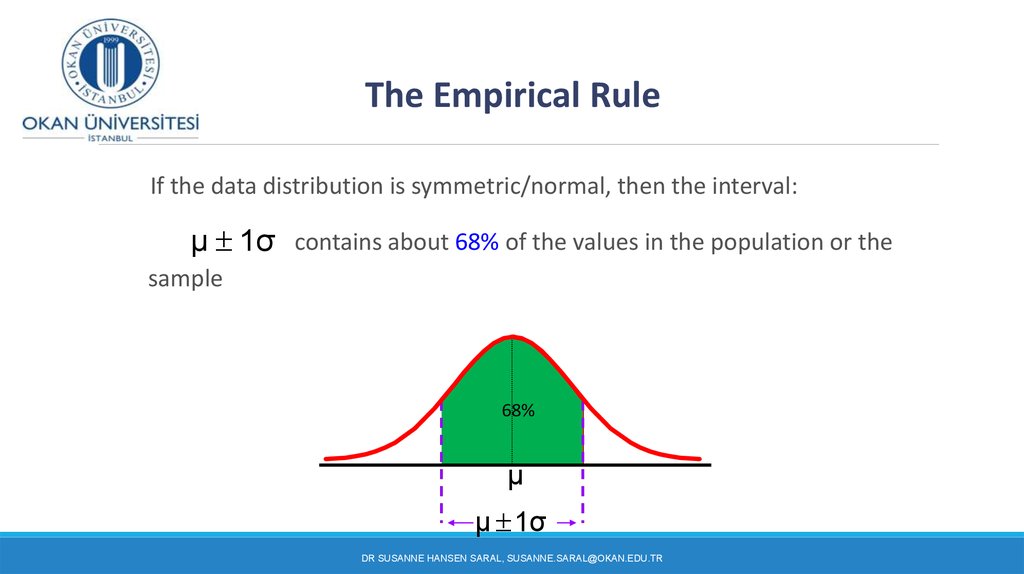
Because of the symmetry of the distribution, half of this 95% is above the mean and half is below. The empirical rule, or the 68-95-99.7 rule, tells you where most of your values lie in a normal distribution: Around 68 of values are within 1 standard deviation from the mean.
The empirical rule says that approximately 95% of data lies within 2 standard deviations of the mean. To calculate the percentage of data values in the shaded region, should we add to or subtract from the 50% of the data that is below the mean? Add Step 3: In the previous step, we determined that we need to add to the 50% of the data that is below the mean in order to calculate the percentage of data values in the region shaded on the graph to the right. Since the bell-shaped distribution is symmetric, around 50% of the data is below the mean. Thus, we want to find the percentage of data values in the region shaded on the graph of the standard normal curve to the right. Step 1: 11.03 - 8.11 / 1.46 = 2 Step 2: This means that 11.03 lies 2 standard deviations above the mean. Normal Distribution Empirical Rule Percentages The normal distribution empirical rule is a set of percentages that explains how much of the data is found within each standard deviation away. According to Chebyshev's Theorem, what is the minimum percentage of data values that lie within 2 standard deviations of the mean? 75% The empirical rule (also called the 'three-sigma rule' or the '68-95-99.7 rule') is a statistical rule that states that, for normally distributed data, almost all the data points will fall within three standard deviations on either side of the mean. Finally, to determine the minimum percentage of recently sold homes with prices between $199,600 and $230,400, answer the following question. Note: This is the same calculation that is used to find the standard score, or z-score, of a data value. Then, dividing by the standard deviation, we can convert these differences into numbers of standard deviations.
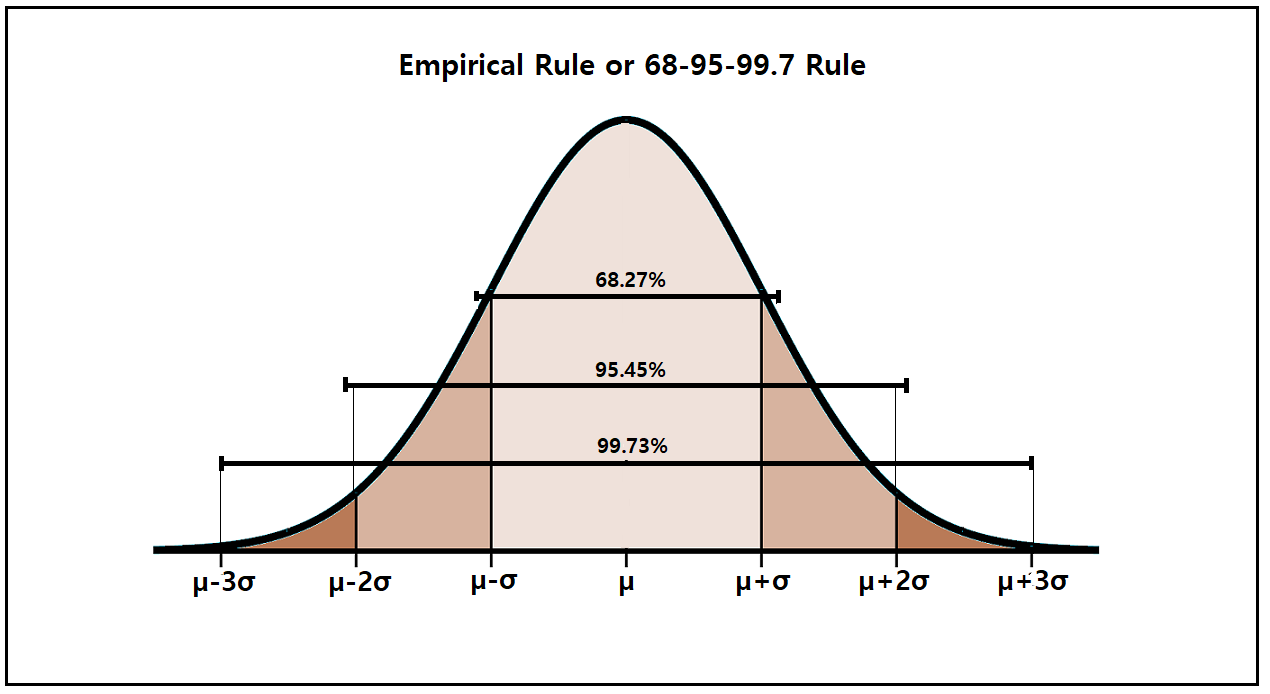
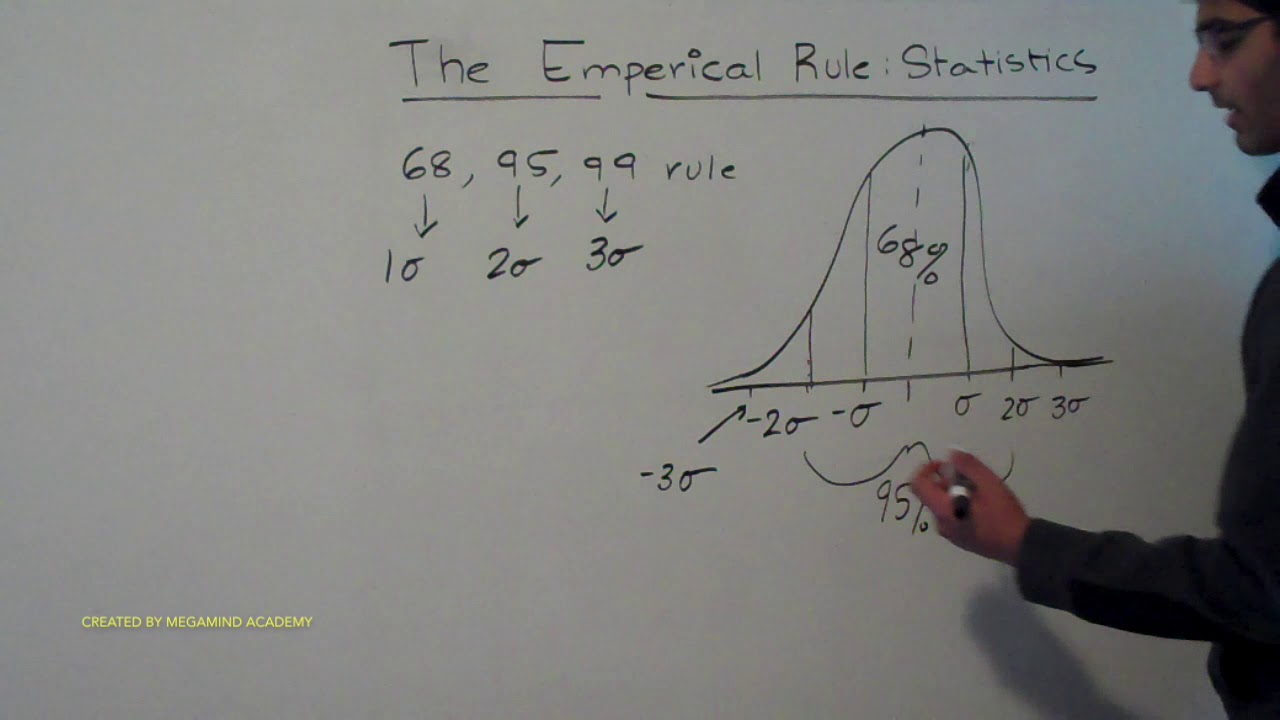
By subtracting, we can find how far each of these figures is from the mean. As the empirical rule requires that all data be only within three deviations, not outside therefore, if a large number of data falls outside the limits of. We need to know how many standard deviations from the mean $199,600 and $230,400 are. In fact, Chebyshev's Theorem may be used for any distribution, regardless of shape, but for bell-shaped distributions, the empirical rule gives a more accurate approximation. Hence, it’s sometimes called the 68 95 and 99.7 rule. When the distribution of a set of data is not known to be bell-shaped, Chebyshev's Theorem can be used to estimate the minimum percentage of values that lie within a few standard deviations of the mean. The Empirical Rule is broken down into three percentages, 68, 95, and 99.7.


 0 kommentar(er)
0 kommentar(er)
